
ก่อนเริ่มกระทู้ ขอแสดงความไว้อาลัยแก่การจากไปของท่านสตีเวน ฮอคกิงครับ


--------------------------------------------------------------
==คณิตศาสตร์ของมนุษย์ต่างดาว จะเหมือนหรือแตกต่างกับคณิตศาสตร์ของมนุษย์ในโลกเราอย่างไร?==
กระทู้ที่ก่อนๆ เราได้เคยสนทนาไปถึงเรื่องที่ว่า คณิตศาสตร์นี้ถูกสร้างขึ้นโดยมนุษย์ หรือมีอยู่แล้วในธรรมชาติแล้วมนุษย์ไปค้นพบมัน?
https://pantip.com/topic/37262917
จึงเป็นเรื่องที่น่าคิดอีกต่อไปว่า สมมติว่ามนุษย์ต่างดาวมีจริง พัฒนาจนอารยธรรมเจริญ แน่นอนเขาก็ต้องมีความรู้ด้านต่างๆ แล้วความรู้ของพวกมนุษย์ต่างดาวเช่นวิชาคณิตศาสตร์นั้น จะเหมือนหรือแตกต่างกับคณิตศาสตร์ที่มนุษย์ใช้กันในโลกนี้อย่างไร เรื่องนี้น่าสงสัยยิ่งนัก

จากกระทู้เก่าจะเห็นว่ามีแนวคิด 2 สายหลัก
1.)สายแรกเชื่อว่าคณิตศาสตร์คือการสร้างขึ้นของสังคมมนุษย์ เรียกว่าเป็น Social construct แนวคิดนี้เช่น Fictionalism เชื่อกันว่าคณิตศาสตร์เป็นเรื่องสมมติ ผู้สนับสนุนแนวคิดนี้คือ Hartry Field เขาบอกว่า 1+1=2 ก็มีความเป็นจริงเท่ากับ เชอลอคโฮมอาศัยอยู่ที่ถนนเบเกอร์ ถามว่า ทั้งสองอย่างนี้เป็นจริงไหมในโลกแห่งความจริงคำถอบคือไม่ แต่ในนิยายถามว่าเชอลอคโฮมอาศัยอยู่ที่ถนนเบเกอร์จริงไหม คำตอบคือจริง ถ้าเป็นในนวนิยาย เชอลอคโฮมในนวนิยายไม่ได้อาศัยอยู่ถนนสุขุมวิท Hartry Field เขาก็เชื่อว่า 1+1 = 2 นั้นก็เป็นจริงในโลกที่เราสมมติขึ้นมาเพื่อความสะดวกในการอธิบายระบบต่างๆที่ซับซ้อน แต่มันไม่ได้มีอยู่ในโลกจริงๆ Hartry Field พยายามจะไม่ใช้คณิตศาสตร์ในวิทยาศาสตร์ด้วย เขาเขียนหนังสือเรื่อง Science Without Numbers
2.)อีกสายหนึ่งเชื่อว่า คณิตศาสตร์นั้นมีอยู่แล้วในเอกภพ นั่นคือแนวคิด Platonism คือ ทรรศนะที่ถือว่า มีสภาพความจริงอีกอย่างหนึ่งที่ไม่ใช่วัตถุ เรียกว่า มโนภาพ(Idea) หรือแบบ(Form) ซึ่งโพลโตถือว่าเป็นจริงและสำคัญกว่าวัตถุ ในปรัชญาคณิตศาสตร์นี้เชื่อว่า คณิตศาสตร์นั้นมนุษย์ไม่ใช่ผู้สร้างมัน แต่เป็นแค่ผู้ค้นพบมัน มันมีอยู่แล้วในธรรมชาติ มีโลกอีกโลกหนึ่งซึ่งเป็นโลกของคณิตศาสตร์ ที่ดำรงอยู่ไม่ขึ้นกับเวลาและ space
แนวคิด Platonism ชื่อก็ตามตัวว่าเป็นแนวคิดของเพลโต นักปรัชญาชาวกรีกโบราณเมื่อประมาณสองพันปีที่แล้ว เขาได้รับอิทธิพลจากแนวคิดของท่านปีทาโกรัสอีกทอดหนึ่ง โดยนำมาอัพเดตใหม่นิดหน่อย ของปีทาโกรัสนั้น เราเรียกว่า แนวคิดแบบ Pythagoreanism ซึ่งเชื่อว่า ทุกอย่างคือตัวเลข ซึ่งทั้ง แนวคิด Platonism และ Pythagoreanism นี่เรียกรวมๆหมวดใหญ่ว่าเป็น Mathematicism ซึ่งถือว่า ทุกอย่างสามารถอธิบาย สร้างเป็นแบบจำลอง ได้ด้วยคณิตศาสตร์
------------------------
สิ่งสำคัญคือแนวคิดแบบ Platonism ที่ว่าคณิตศาสตร์นั้นมนุษย์ไปค้นพบ มันมีอยู่แล้วในธรรมชาติ ถ้าเป็นแบบนี้ โอกาสที่มนุษย์ต่างดาวจะมีคณิตศาสตร์เหมือนเราก็มีความเป็นไปได้ แต่มันอาจจะไม่ง่ายอย่างนั้น เพราะมองมาที่โลกมนุษย์เราเอง คณิตศาสตร์ สัญลักษณ์ วิธีคิดต่างๆในอดีตเวลาพูดถึงคณิตศาสตร์ มนุษย์ในปัจจุบันไปอ่านแล้วก็อาจจะงง เช่นกัน นักคณิตศาสตร์ในอดีตเมื่อพันกว่าปีที่แล้วมาเจอเลขในปัจจุบันก็อาจจะงง สับสนเช่นกัน มันมีการมอง การถ่ายทอด วิธีคิด สื่อได้หลายแบบ ก่อนจะพูดถึงมนุษย์ต่างดาว ยกตัวอย่างมาที่โลกของเราก่อนดีกว่า

ระบบเลขที่เราใช้กันอยู่ทุกวันนี้เรียกว่า ระบบเลขฮินดูอารบิก คือคาดว่าเกิดขึ้นที่ในอินเดียซึ่งนับถือศาสนาฮินดูและติดต่อผ่านการค้าขาย พวกอาหรับรับไปใช้และแพร่ไปในยุโรป ยุโรปในสมัยก่อนนั้นยังใช้ระบบเลขโรมันซึ่งต่างจากระบบเลขฮินดูอารบิกอย่างสิ้นเชิง เช่น 1952 เขียนเป็นเลขโรมันได้เป็น MCMLII (ตอนดูหนังฮอลลีวูดเก่าๆตอนเครดิตจะบอกปีที่หนังสร้างซึ่งเขียนเป็นเลขโรมัน ดูหนังจนจบแล้วลองฝึกแปลงมาเป็นเลขในปัจจุบันถือว่าสนุกดี) และเลข 58 เขียนได้เป็น LVIII สมัยก่อน คนใช้เลขกันในระบบนี้ คิดดูว่าเวลาเอามาคูณกัน หารกันมันจะยาก งง แค่ไหนเช่น 1952*58 = ? เราก็คูณกันแบบที่เรียนมา แต่ลองเป็นเลขโรมัน จะได้ MCMLII*LVIII =? เวลาเอามาคูณกันจะดูสับสนงุนงงยิ่ง ลำบากต่อการคิดมากๆ
แล้วก็มีหนุ่มสุดหล่อนามว่า ฟิโบนักชี

Fibonacci
ใช่แล้วฟีโบนักชีคนเดียวกับที่โด่งดังเรื่องลำดับฟีโบนักชี (Fibonacci sequence)
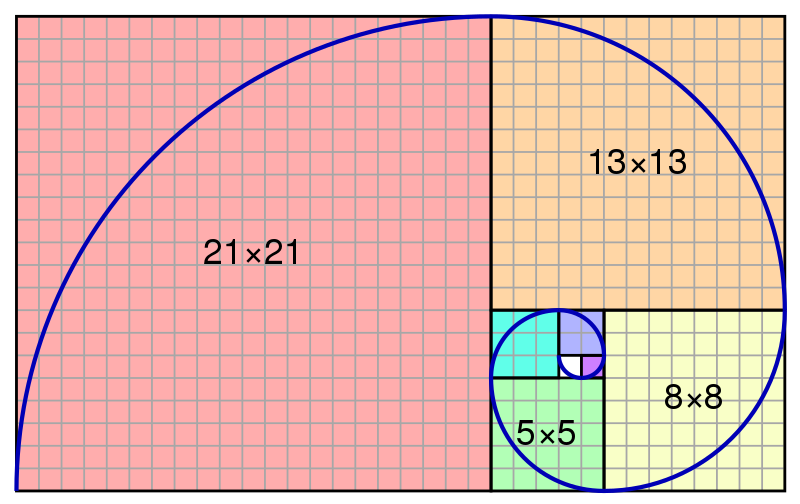

ในหนังสือของฟีโนนักชี ชื่อเรื่อง Liber Abaci ตีพิมพ์ปี 1202 ถือเป็นการแนะนำการใช้เลขศูนย์และระบบเลขฮินดูอารบิกแทนระบบเลขโรมันในยุโรป แล้วทุกอย่างก็ง่ายขึ้นมาก พ่อค้าแม่ค้า คำนวณ บวกลบคูณหารเลขได้ง่ายดายกว่าเดิมมาก เริ่มมีการใช้ระบบเลขฮินดูอารบิกในยุโรปในศตวรรษที่ 12 และเป็นที่นิยมทั่วไปในศตวรรษที่ 15 ต้องขอบคุณท่านฟิโบนักชีมากที่แนะนำระบบนี้แทนระบบเก่าของโรมัน มันทำให้ทุกอย่างง่ายสะดวกขึ้นมาก ส่งผลกระทบสำคัญต่อการพัฒนาวิทยาศาสตร์และคณิตศาสตร์ในยุคต่อมา และการค้าขาย คำนวณสิ่งต่างๆก็ง่ายขึ้น สะดวก รวดเร็วขึ้น
ระบบตัวเลขแค่ในโลกนี้ยังมีมากมายหลากหลาย เช่น ระบบเลขฮินดูอารบิก ระบบเลขโรมัน ระบบเลขบาบิโลน ระบบเลขอียิปต์ แค่ในโลกเรายังมีตั้งมากมาย หลากหลาย นั้นระบบเลขของมนุษย์ต่างดาวก็อาจจะไม่เหมือนกับที่เราใช้อยู่ก็เป็นได้
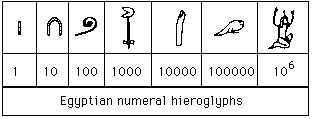
ระบบเลขอียิปต์
นอกจากระบบตัวเลขแล้วยังมีเรื่องของฐาน (radix หรือ base) เช่นระบบเลขฮินดุอารบิกนั้นเป็นเลขฐานสิบ คาดว่ามนุษย์นิยมใช้เลขฐานสิบเพราะมีนิ้วที่มือทั้งหมดสิบนิ้ว แต่ก็ยังมีฐานอื่นๆอีกเช่น ในอดีตชาวสุเมเรียนใช้ฐาน 60 บางอารยธรรมก็ใช้ฐานสิบสอง ซึ่งส่งผลมาหลายอย่างจนถึงปัจจุบันเช่น ราศีมี 12 ราศี ชาวบาบิโลน 1 วันมี 12 ชั่วโมง ซึ่งต่อมาก็กลายเป็น 24 ชั่วโมง , โหล , หน่วยอิมพีเรียลที่ 1 ฟุตมี 12 นิ้ว เป็นต้น
อย่างด้านคอมพิวเตอร์ก็นิยมใช้เลขฐานสอง เพราะสะดวกดีมีแค่ 0 กับ 1 เวลาส่งสัญญาณ และยังมีระบบเลขฐาน 1 (Unary numeral system) บางศาสตร์บางสาขาก็ใช้ เช่น 5 ก็คือ ///// หรือ 3 ก็คือ ///

ศึก 12 ราศี
นั้นก็พอจะเป็นไปได้ว่าถ้ามนุษย์ต่างดาวมีนิ้วมือทั้งหมด 8 นิ้ว แบบในหนังเรื่อง อี.ที. เพื่อนรัก (E.T. the Extra-Terrestrial) หนังของสปีลเบิกปี 1982 ก็จะอาจใช้เลขฐาน 8 หรือถ้ามนุาย์ต่างดาวมี 14 นิ้วก็อาจใช้เลขฐาน 14 ก็เป็นไปได้

ไม่เพียงแค่นั้น วิธีการคิดการมองคณิตศาสตร์ก็อาจแตกต่างกันได้ด้วย เช่น ย้อนกลับไปในยุคกรีกโบราณ ชาวกรีกเขามองเข้าใจการคูณว่า คือ สี่เหลี่ยมผืนผ้า rectangle (จริงๆจะมองเป็นสีเหลี่ยมจัตุรัสด้วยก็ได้ ถ้ามันคือเลขเดียวกัน) อย่างเช่นในรูปด้านล่าง
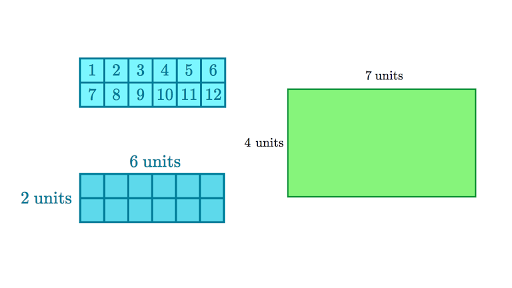
รูปด้านซ้าย คือการคูณกันของ 2 คูณกับ 6 ก็จะได้ 12 ชาวกรีกเขามองการคูณกันเป็นแบบนี้ หรือรูปทางขวา ก็คือการนำ 7 คูณกับ 4 ชาวกรีกเขามองการคูณกันเป็นภาพแบบนี้ซึ่งมันก็เจ๋งดี เช่น การพิสูจน์ว่า (a+b)^2 = a^2+ 2ab + b^2 การมองด้วยรูปภาพแบบชาวกรีกจะเห็นได้อย่างชัดเจนดังรูปด้านล่าง
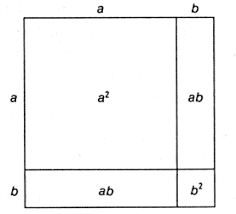
เราจะได้ไม่คิดผิด

แต่การคิดแบบนี้บางทีมันก็เกิดปัญหา เช่นเลขสองตัวคูณกันมองเป็น พื้นที่ เลขสามตัวคูณกันมองเป็นปริมาตร
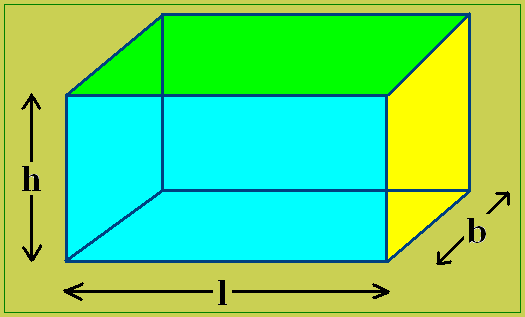
Rectangular cuboid
แต่ถ้าการคูณกันมากกว่า 3 ตัวหล่ะ เช่น การคูณกัน ของ 2*3*5*4 จะมองได้เป็นรูปทรงอะไร ?
ชาวกรีกเจอการคูณกันของเลขมากกว่า 3 ตัว แล้วงุนงง สับสน

เพราะเราอยู่ในเอกภพที่ปริภูมิมี 3 มิติ นั้นเราจึงจินตนาการการคูณกันของตัวเลขที่มากกว่า 3 ตัวเป็นรูปร่างไม่ได้ นี่คือข้อเสียของการมองการคูณเป็นรูปภาพของชาวกรีก
การนิยามการคูณกันของชาวกรีกยังใช้แบบนี้เรื่อยมา ในงานเขียนของนิวตันก็ยังพบว่า rectangular (สี่เหลี่ยมผืนผ้า) ใช้ในความหมายของการคูณ จนมาสู่ยุคหลังๆ มีการนิยามการคูณแบบใหม่ ทำให้ไม่เกิดปัญหา จะคูณกันกี่ครั้งก็ได้ นี่จึงเป็นสิ่งที่น่าสนใจจะเห็นว่าแม้แต่การคูณกัน ยังมองได้หลายแบบ มนุษย์ต่างดาวอาจจะมองคณิตศาสตร์เรื่องเดียวกันของเราในมุมที่ต่างออกไปก็ได้
-----------------------------
เดี๋ยวมาเขียนต่อครับ ถ้าชอบช่วยกดบวก กดถูกใจด้วยนะครับ ขอบคุณครับ
- จขกท. สุดหล่อ


==คณิตศาสตร์ของมนุษย์ต่างดาว จะเหมือนหรือแตกต่างกับคณิตศาสตร์ของมนุษย์ในโลกเราอย่างไร?==
ก่อนเริ่มกระทู้ ขอแสดงความไว้อาลัยแก่การจากไปของท่านสตีเวน ฮอคกิงครับ
--------------------------------------------------------------
==คณิตศาสตร์ของมนุษย์ต่างดาว จะเหมือนหรือแตกต่างกับคณิตศาสตร์ของมนุษย์ในโลกเราอย่างไร?==
กระทู้ที่ก่อนๆ เราได้เคยสนทนาไปถึงเรื่องที่ว่า คณิตศาสตร์นี้ถูกสร้างขึ้นโดยมนุษย์ หรือมีอยู่แล้วในธรรมชาติแล้วมนุษย์ไปค้นพบมัน?
https://pantip.com/topic/37262917
จึงเป็นเรื่องที่น่าคิดอีกต่อไปว่า สมมติว่ามนุษย์ต่างดาวมีจริง พัฒนาจนอารยธรรมเจริญ แน่นอนเขาก็ต้องมีความรู้ด้านต่างๆ แล้วความรู้ของพวกมนุษย์ต่างดาวเช่นวิชาคณิตศาสตร์นั้น จะเหมือนหรือแตกต่างกับคณิตศาสตร์ที่มนุษย์ใช้กันในโลกนี้อย่างไร เรื่องนี้น่าสงสัยยิ่งนัก
จากกระทู้เก่าจะเห็นว่ามีแนวคิด 2 สายหลัก
1.)สายแรกเชื่อว่าคณิตศาสตร์คือการสร้างขึ้นของสังคมมนุษย์ เรียกว่าเป็น Social construct แนวคิดนี้เช่น Fictionalism เชื่อกันว่าคณิตศาสตร์เป็นเรื่องสมมติ ผู้สนับสนุนแนวคิดนี้คือ Hartry Field เขาบอกว่า 1+1=2 ก็มีความเป็นจริงเท่ากับ เชอลอคโฮมอาศัยอยู่ที่ถนนเบเกอร์ ถามว่า ทั้งสองอย่างนี้เป็นจริงไหมในโลกแห่งความจริงคำถอบคือไม่ แต่ในนิยายถามว่าเชอลอคโฮมอาศัยอยู่ที่ถนนเบเกอร์จริงไหม คำตอบคือจริง ถ้าเป็นในนวนิยาย เชอลอคโฮมในนวนิยายไม่ได้อาศัยอยู่ถนนสุขุมวิท Hartry Field เขาก็เชื่อว่า 1+1 = 2 นั้นก็เป็นจริงในโลกที่เราสมมติขึ้นมาเพื่อความสะดวกในการอธิบายระบบต่างๆที่ซับซ้อน แต่มันไม่ได้มีอยู่ในโลกจริงๆ Hartry Field พยายามจะไม่ใช้คณิตศาสตร์ในวิทยาศาสตร์ด้วย เขาเขียนหนังสือเรื่อง Science Without Numbers
2.)อีกสายหนึ่งเชื่อว่า คณิตศาสตร์นั้นมีอยู่แล้วในเอกภพ นั่นคือแนวคิด Platonism คือ ทรรศนะที่ถือว่า มีสภาพความจริงอีกอย่างหนึ่งที่ไม่ใช่วัตถุ เรียกว่า มโนภาพ(Idea) หรือแบบ(Form) ซึ่งโพลโตถือว่าเป็นจริงและสำคัญกว่าวัตถุ ในปรัชญาคณิตศาสตร์นี้เชื่อว่า คณิตศาสตร์นั้นมนุษย์ไม่ใช่ผู้สร้างมัน แต่เป็นแค่ผู้ค้นพบมัน มันมีอยู่แล้วในธรรมชาติ มีโลกอีกโลกหนึ่งซึ่งเป็นโลกของคณิตศาสตร์ ที่ดำรงอยู่ไม่ขึ้นกับเวลาและ space
แนวคิด Platonism ชื่อก็ตามตัวว่าเป็นแนวคิดของเพลโต นักปรัชญาชาวกรีกโบราณเมื่อประมาณสองพันปีที่แล้ว เขาได้รับอิทธิพลจากแนวคิดของท่านปีทาโกรัสอีกทอดหนึ่ง โดยนำมาอัพเดตใหม่นิดหน่อย ของปีทาโกรัสนั้น เราเรียกว่า แนวคิดแบบ Pythagoreanism ซึ่งเชื่อว่า ทุกอย่างคือตัวเลข ซึ่งทั้ง แนวคิด Platonism และ Pythagoreanism นี่เรียกรวมๆหมวดใหญ่ว่าเป็น Mathematicism ซึ่งถือว่า ทุกอย่างสามารถอธิบาย สร้างเป็นแบบจำลอง ได้ด้วยคณิตศาสตร์
------------------------
สิ่งสำคัญคือแนวคิดแบบ Platonism ที่ว่าคณิตศาสตร์นั้นมนุษย์ไปค้นพบ มันมีอยู่แล้วในธรรมชาติ ถ้าเป็นแบบนี้ โอกาสที่มนุษย์ต่างดาวจะมีคณิตศาสตร์เหมือนเราก็มีความเป็นไปได้ แต่มันอาจจะไม่ง่ายอย่างนั้น เพราะมองมาที่โลกมนุษย์เราเอง คณิตศาสตร์ สัญลักษณ์ วิธีคิดต่างๆในอดีตเวลาพูดถึงคณิตศาสตร์ มนุษย์ในปัจจุบันไปอ่านแล้วก็อาจจะงง เช่นกัน นักคณิตศาสตร์ในอดีตเมื่อพันกว่าปีที่แล้วมาเจอเลขในปัจจุบันก็อาจจะงง สับสนเช่นกัน มันมีการมอง การถ่ายทอด วิธีคิด สื่อได้หลายแบบ ก่อนจะพูดถึงมนุษย์ต่างดาว ยกตัวอย่างมาที่โลกของเราก่อนดีกว่า
ระบบเลขที่เราใช้กันอยู่ทุกวันนี้เรียกว่า ระบบเลขฮินดูอารบิก คือคาดว่าเกิดขึ้นที่ในอินเดียซึ่งนับถือศาสนาฮินดูและติดต่อผ่านการค้าขาย พวกอาหรับรับไปใช้และแพร่ไปในยุโรป ยุโรปในสมัยก่อนนั้นยังใช้ระบบเลขโรมันซึ่งต่างจากระบบเลขฮินดูอารบิกอย่างสิ้นเชิง เช่น 1952 เขียนเป็นเลขโรมันได้เป็น MCMLII (ตอนดูหนังฮอลลีวูดเก่าๆตอนเครดิตจะบอกปีที่หนังสร้างซึ่งเขียนเป็นเลขโรมัน ดูหนังจนจบแล้วลองฝึกแปลงมาเป็นเลขในปัจจุบันถือว่าสนุกดี) และเลข 58 เขียนได้เป็น LVIII สมัยก่อน คนใช้เลขกันในระบบนี้ คิดดูว่าเวลาเอามาคูณกัน หารกันมันจะยาก งง แค่ไหนเช่น 1952*58 = ? เราก็คูณกันแบบที่เรียนมา แต่ลองเป็นเลขโรมัน จะได้ MCMLII*LVIII =? เวลาเอามาคูณกันจะดูสับสนงุนงงยิ่ง ลำบากต่อการคิดมากๆ
แล้วก็มีหนุ่มสุดหล่อนามว่า ฟิโบนักชี
Fibonacci
ใช่แล้วฟีโบนักชีคนเดียวกับที่โด่งดังเรื่องลำดับฟีโบนักชี (Fibonacci sequence)
ในหนังสือของฟีโนนักชี ชื่อเรื่อง Liber Abaci ตีพิมพ์ปี 1202 ถือเป็นการแนะนำการใช้เลขศูนย์และระบบเลขฮินดูอารบิกแทนระบบเลขโรมันในยุโรป แล้วทุกอย่างก็ง่ายขึ้นมาก พ่อค้าแม่ค้า คำนวณ บวกลบคูณหารเลขได้ง่ายดายกว่าเดิมมาก เริ่มมีการใช้ระบบเลขฮินดูอารบิกในยุโรปในศตวรรษที่ 12 และเป็นที่นิยมทั่วไปในศตวรรษที่ 15 ต้องขอบคุณท่านฟิโบนักชีมากที่แนะนำระบบนี้แทนระบบเก่าของโรมัน มันทำให้ทุกอย่างง่ายสะดวกขึ้นมาก ส่งผลกระทบสำคัญต่อการพัฒนาวิทยาศาสตร์และคณิตศาสตร์ในยุคต่อมา และการค้าขาย คำนวณสิ่งต่างๆก็ง่ายขึ้น สะดวก รวดเร็วขึ้น
ระบบตัวเลขแค่ในโลกนี้ยังมีมากมายหลากหลาย เช่น ระบบเลขฮินดูอารบิก ระบบเลขโรมัน ระบบเลขบาบิโลน ระบบเลขอียิปต์ แค่ในโลกเรายังมีตั้งมากมาย หลากหลาย นั้นระบบเลขของมนุษย์ต่างดาวก็อาจจะไม่เหมือนกับที่เราใช้อยู่ก็เป็นได้
ระบบเลขอียิปต์
นอกจากระบบตัวเลขแล้วยังมีเรื่องของฐาน (radix หรือ base) เช่นระบบเลขฮินดุอารบิกนั้นเป็นเลขฐานสิบ คาดว่ามนุษย์นิยมใช้เลขฐานสิบเพราะมีนิ้วที่มือทั้งหมดสิบนิ้ว แต่ก็ยังมีฐานอื่นๆอีกเช่น ในอดีตชาวสุเมเรียนใช้ฐาน 60 บางอารยธรรมก็ใช้ฐานสิบสอง ซึ่งส่งผลมาหลายอย่างจนถึงปัจจุบันเช่น ราศีมี 12 ราศี ชาวบาบิโลน 1 วันมี 12 ชั่วโมง ซึ่งต่อมาก็กลายเป็น 24 ชั่วโมง , โหล , หน่วยอิมพีเรียลที่ 1 ฟุตมี 12 นิ้ว เป็นต้น
อย่างด้านคอมพิวเตอร์ก็นิยมใช้เลขฐานสอง เพราะสะดวกดีมีแค่ 0 กับ 1 เวลาส่งสัญญาณ และยังมีระบบเลขฐาน 1 (Unary numeral system) บางศาสตร์บางสาขาก็ใช้ เช่น 5 ก็คือ ///// หรือ 3 ก็คือ ///
ศึก 12 ราศี
นั้นก็พอจะเป็นไปได้ว่าถ้ามนุษย์ต่างดาวมีนิ้วมือทั้งหมด 8 นิ้ว แบบในหนังเรื่อง อี.ที. เพื่อนรัก (E.T. the Extra-Terrestrial) หนังของสปีลเบิกปี 1982 ก็จะอาจใช้เลขฐาน 8 หรือถ้ามนุาย์ต่างดาวมี 14 นิ้วก็อาจใช้เลขฐาน 14 ก็เป็นไปได้
ไม่เพียงแค่นั้น วิธีการคิดการมองคณิตศาสตร์ก็อาจแตกต่างกันได้ด้วย เช่น ย้อนกลับไปในยุคกรีกโบราณ ชาวกรีกเขามองเข้าใจการคูณว่า คือ สี่เหลี่ยมผืนผ้า rectangle (จริงๆจะมองเป็นสีเหลี่ยมจัตุรัสด้วยก็ได้ ถ้ามันคือเลขเดียวกัน) อย่างเช่นในรูปด้านล่าง
รูปด้านซ้าย คือการคูณกันของ 2 คูณกับ 6 ก็จะได้ 12 ชาวกรีกเขามองการคูณกันเป็นแบบนี้ หรือรูปทางขวา ก็คือการนำ 7 คูณกับ 4 ชาวกรีกเขามองการคูณกันเป็นภาพแบบนี้ซึ่งมันก็เจ๋งดี เช่น การพิสูจน์ว่า (a+b)^2 = a^2+ 2ab + b^2 การมองด้วยรูปภาพแบบชาวกรีกจะเห็นได้อย่างชัดเจนดังรูปด้านล่าง
เราจะได้ไม่คิดผิด
แต่การคิดแบบนี้บางทีมันก็เกิดปัญหา เช่นเลขสองตัวคูณกันมองเป็น พื้นที่ เลขสามตัวคูณกันมองเป็นปริมาตร
Rectangular cuboid
แต่ถ้าการคูณกันมากกว่า 3 ตัวหล่ะ เช่น การคูณกัน ของ 2*3*5*4 จะมองได้เป็นรูปทรงอะไร ?
ชาวกรีกเจอการคูณกันของเลขมากกว่า 3 ตัว แล้วงุนงง สับสน
เพราะเราอยู่ในเอกภพที่ปริภูมิมี 3 มิติ นั้นเราจึงจินตนาการการคูณกันของตัวเลขที่มากกว่า 3 ตัวเป็นรูปร่างไม่ได้ นี่คือข้อเสียของการมองการคูณเป็นรูปภาพของชาวกรีก
การนิยามการคูณกันของชาวกรีกยังใช้แบบนี้เรื่อยมา ในงานเขียนของนิวตันก็ยังพบว่า rectangular (สี่เหลี่ยมผืนผ้า) ใช้ในความหมายของการคูณ จนมาสู่ยุคหลังๆ มีการนิยามการคูณแบบใหม่ ทำให้ไม่เกิดปัญหา จะคูณกันกี่ครั้งก็ได้ นี่จึงเป็นสิ่งที่น่าสนใจจะเห็นว่าแม้แต่การคูณกัน ยังมองได้หลายแบบ มนุษย์ต่างดาวอาจจะมองคณิตศาสตร์เรื่องเดียวกันของเราในมุมที่ต่างออกไปก็ได้
-----------------------------
เดี๋ยวมาเขียนต่อครับ ถ้าชอบช่วยกดบวก กดถูกใจด้วยนะครับ ขอบคุณครับ
- จขกท. สุดหล่อ