คำตอบที่ได้รับเลือกจากเจ้าของกระทู้
ความคิดเห็นที่ 1
การคำนวณด้วยวิธีสมดุลของแรง mv2/r = GMm/r2 นี้
มันคือนิยามของความเร็วโคจรรอบโลก ครับ
คือ ให้แรงจากความโน้มถ่วงโลก
มีค่าเท่ากับแรงเทียมหนีศูนย์ (Centrifugal force)
ก็จะได้เป็นความเร็วที่วัตถุจะสามารถ
รักษาการโคจรรอบโลกเป็นวงกลม
ณ รัศมี r จากใจกลางโลกได้
ส่วนความเร็ว Escape velocity นั้น
จะต้องคำนวณแบบแรกที่ท่านทำครับ
คือ ใช้กฎการอนุรักษ์พลังงาน
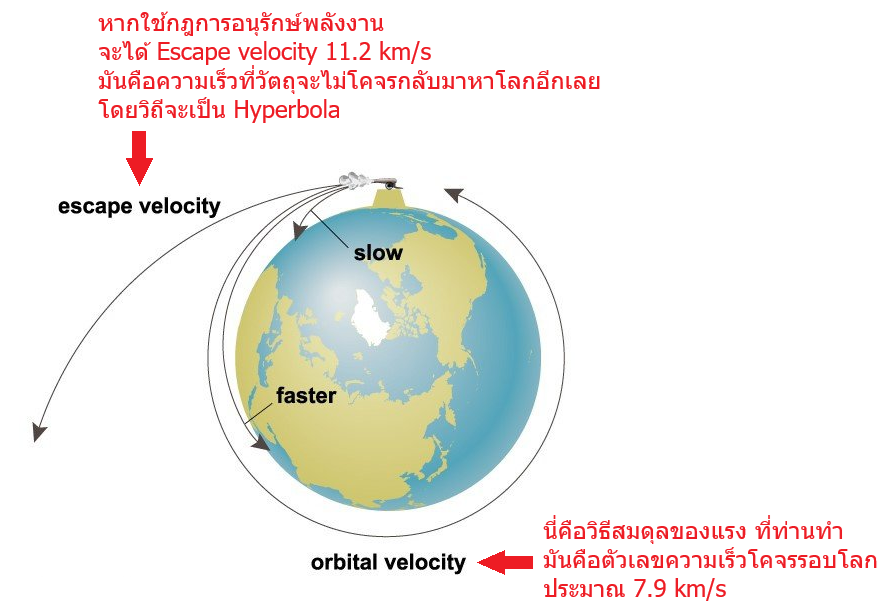
หากใช้ความเร็วมากกว่า 7.9 แต่ไม่ถึง 11.2 km/s
วัตถุจะยังโคจรรอบโลกเป็นวงรี ได้
แต่หากความเร็วเกิน 11.2 km/s
มันจะกลายเป็น Hyperbola ไปเลยครับ
จะไม่วกกลับมายังโลกอีกแล้ว
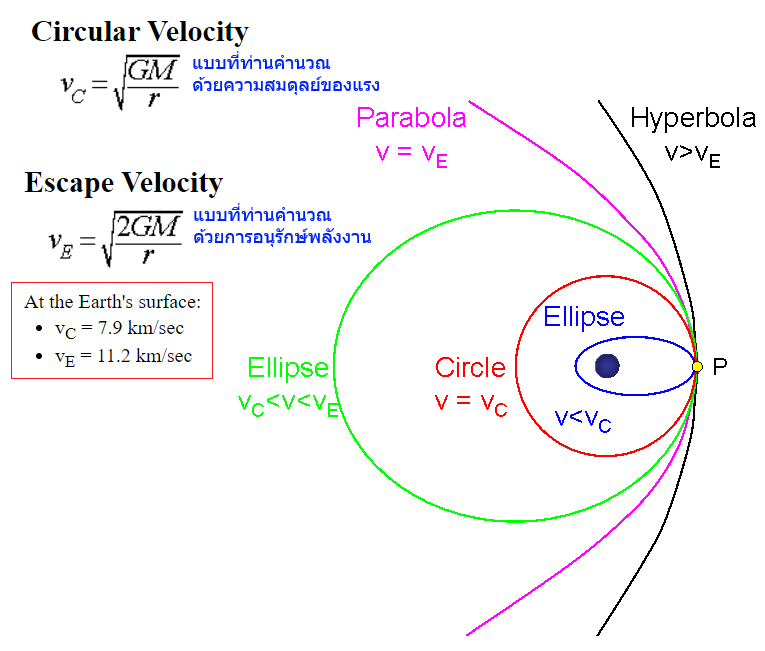
มันคือนิยามของความเร็วโคจรรอบโลก ครับ
คือ ให้แรงจากความโน้มถ่วงโลก
มีค่าเท่ากับแรงเทียมหนีศูนย์ (Centrifugal force)
ก็จะได้เป็นความเร็วที่วัตถุจะสามารถ
รักษาการโคจรรอบโลกเป็นวงกลม
ณ รัศมี r จากใจกลางโลกได้
ส่วนความเร็ว Escape velocity นั้น
จะต้องคำนวณแบบแรกที่ท่านทำครับ
คือ ใช้กฎการอนุรักษ์พลังงาน

หากใช้ความเร็วมากกว่า 7.9 แต่ไม่ถึง 11.2 km/s
วัตถุจะยังโคจรรอบโลกเป็นวงรี ได้
แต่หากความเร็วเกิน 11.2 km/s
มันจะกลายเป็น Hyperbola ไปเลยครับ
จะไม่วกกลับมายังโลกอีกแล้ว

▼ กำลังโหลดข้อมูล... ▼
แสดงความคิดเห็น
คุณสามารถแสดงความคิดเห็นกับกระทู้นี้ได้ด้วยการเข้าสู่ระบบ



ทำไมความเร็วหลุดพ้นโลกที่คำนวณด้วยวิธีอื่นจึงไม่เท่ากัน (11.2m/s กับ 7.9m/s)
K1 + U1 = K2 + U2
โดยที่
K1 = (1/2)(mv1^2)
U1 = -GMm/r1
K2 = (1/2)(mv2^2)
U2 = -GMm/r2
โดย
G คือ ค่าความโน้มถ่วงสากล = 6.67x10^-11 N-m^2/kg^2
v1 คือความเร็วหลุดพ้นที่เราต้องการหาค่า
v2 = 0
r1 คือ รัศมีของโลก = 6,371,000 เมตร
r2 = infinity
ด้วยวิธีนี้ ปรากฎว่าได้ความเร็วหลุดพ้นประมาณ 11.2 กิโลเมตรต่อวินาที
อีกวิธี
ผมลองคำนวณด้วยวิธีสมดุลของแรง โดยให้แรงหนีศูนย์กลางจากการบินรอบโลกด้วยความเร็วสูง เท่ากับ แรงโน้มถ่วงของโลก ดังนี้
mv^2/r = GMm/r^2
โดยที่
v คือความเร็วหลุดพ้นที่เราต้องการหาค่า
r คือ รัศมีของโลก = 6,371,000 เมตร
M คือ มวลของโลก = 5.97x10^24 กิโลกรัม
และบินใกล้ผิวโลกโดยไม่มีแรงต้านจากอากาศ
ด้วยวิธีนี้ ปรากฎว่าได้ความเร็วหลุดพ้นประมาณ 7.9 กิโลเมตรต่อวินาที
อยากทราบว่า ทำไมผลลัพธ์ที่ได้จึงต่างกันขนาดนี้ วิธีสมดุลของแรง เป็นวิธีที่ผิดหรือไม่ อย่างไรครับ