ความถี่คืออะไร
https://th.wikipedia.org/wiki/%E0%B8%84%E0%B8%A7%E0%B8%B2%E0%B8%A1%E0%B8%96%E0%B8%B5%E0%B9%88
โน้ตดนตรีคืออะไร
https://th.wikipedia.org/wiki/%E0%B9%82%E0%B8%99%E0%B9%89%E0%B8%95%E0%B8%94%E0%B8%99%E0%B8%95%E0%B8%A3%E0%B8%B5
แล้วอนันต์คืออะไร (ในกรณีนี้ ไม่เกี่ยวข้องใดๆกับคนที่ชื่ออนันต์ทั้งสิ้น)
https://th.wikipedia.org/wiki/%E0%B8%AD%E0%B8%99%E0%B8%B1%E0%B8%99%E0%B8%95%E0%B9%8C
และที่ไม่น่าเชื่อ แต่ก็ต้องเชื่อ เพราะมันเกิดขึ้นจริง พิสูจน์โดยผมเอง แม้จะเป็นแค่เชิงทฤษฎีก็ตาม
ผมสามารถก้าวผ่านความอนันต์ได้ครับ โดยค้นพบจากสูตรที่เกี่ยวข้องกับความถี่และโน้ตดนตรี มันดูเหมือนจะเพ้อเจ้อสำหรับคนที่ไม่เชื่อเรื่องเหนือธรรมชาติ เพราะ ทุกสรรพสิ่งมีค่าเป็นอนันต์ ทุกอย่างที่มันเป็นไป มีเบื้องหลังคือพลังงานเสมอ แม้แต่เหตุการณ์ก่อนเกิดจักรวาลก็ตาม โดยมีเวลาเป็นระยะในความเป็นไปของพลังงาน
ซึ่งถ้าเอาชัดๆ คือ เวลา กับ พลังงาน มีค่าเป็นอนันต์ ไม่มีจุดเริ่มต้นและจุดจบ (ในกรณีที่ไม่ใช่ทฤษฎี beyond) หรือพูดง่ายๆ ก็คือ เป็นอมตะนั่นเอง
ทฤษฎี beyond จะเป็นแบบนี้ครับ สามารถหาจุดจบได้เสมอ แต่ก็สามารถเพิ่มข้อแม้ได้เสมอเช่นกัน เช่น เราค้นพบจุดจบแล้ว แล้วถ้างั้น จุดจบของจุดจบคืออะไร มันก็จะเกทับไปได้เรื่อยๆ เราอย่าพูดว่า จุดจบไม่มีจริง มันมีจริงครับ เพียงแต่ว่ามันเพิ่มข้อแม้ได้ก็เท่านั้นเอง
youtube อันนี้ อธิบายได้ดีมาก (ที่จริงสามารถไปต่อได้อีกนะ แต่เขาเลือกที่จะจบตรงนั้น)
ในคลิปนี้เป็นการก้าวผ่านความอนันต์โดยการเพิ่มข้อแม้จากคำศัพท์ต่างๆ

แต่วันนี้ ผมจะมาก้าวผ่านความอนันต์จากความถี่และโน้ตดนตรีครับผม
เข้าเรื่องจริงๆเสียที
คุณรู้จักความถี่ 440 Hz หรือเปล่า ถ้าใครยังไม่รู้จัก ผมจะอธิบายให้ตรงนี้เลย
มันคือความถี่มาตรฐานสากลของการทำดนตรีเพลงครับผม
เพลงต่างๆที่พวกเราฟังมักจะมีความถี่ 440 Hz
แต่บางคนก็ยึดติดกับ 432 Hz (flat กว่า 440) เพราะมันดูเป็นธรรมชาติกว่า บางคนบอกว่าเป็นความถี่เกี่ยวกับจักรวาล บางคนโยงไปถึงเรื่องลี้ลับ เรื่องศาสนา อะไรแบบเนี้ย ซึ่งก็ไม่รู้ว่าจริงเท็จแต่ประการใด อันนี้ผมไม่มีไอเดีย
โดยส่วนตัวแล้ว ผมก็ชอบหลากหลายครับ ไม่ว่าจะ flat หรือ sharp ก็ตาม ซึ่งมันก็ขึ้นอยู่กับอารมณ์อะนะ
ก่อนที่จะจริงจังไปมากกว่านี้ ก็อยากจะให้คนที่ยังไม่เคยรู้ ได้รู้เอาไว้ ว่า ความถี่ 440 Hz เท่ากับ โน้ต A4 ครับ

โอเค คราวนี้จะเข้มข้นของจริงละ เราจะมาเรียนรู้สูตรที่เกี่ยวข้องกับความถี่และโน้ตดนตรี
โดยวันนี้ ผมจะบอกทั้งหมด 2 สูตร คือ หาค่าความถี่จากโน้ตดนตรี และ หาค่าโน้ตดนตรีจากความถี่ (สูตรกลับ ซึ่งไม่นิยม)
โดยทั้ง 2 สูตรนี้ ต้องกำหนด 440 Hz (A4) เป็นตัวตั้ง
กำหนดให้
f คือ ค่าความถี่ (หน่วยเป็น Hz) และ
n คือ ค่าโน้ตดนตรีที่เพิ่มขึ้นหรือลดลงจาก A4 เป็นหลัก (หน่วยเป็น semitone(s))
****************************************************************************************************************
หาค่าความถี่จากโน้ตดนตรี สูตรคือ
f = 2^(n/12)x440Hz
ตัวอย่างที่ 1
ถ้าอยากรู้ว่า B4 คือความถี่เท่าไร ซึ่ง B4 สูงกว่า A4 อยู่ที่ 2 semitones ให้ทำดังนี้
f = 2^(2/12)x440Hz
f = 493.883301256 Hz
B4 = 493.883301256 Hz
ตัวอย่างที่ 2
คราวนี้เราลองไปไกลบ้าง งั้นเอาสัก F6 เลย ซึ่งสูงกว่า A4 อยู่ที่ 20 semitones ให้ทำดังนี้
f = 2^(20/12)x440Hz
f = 1396.91292573 Hz
F6 = 1396.91292573 Hz
ตัวอย่างที่ 3
ลองไปทางต่ำกันดูบ้าง A1 ก็ละกัน ซึ่งต่ำกว่า A4 อยู่ที่ 36 semitones ให้ทำดังนี้
f = 2^(-36/12)x440Hz
f = 55 Hz
A1 = 55 Hz
****************************************************************************************************************
หาค่าโน้ตดนตรีจากความถี่ (สูตรกลับ ซึ่งไม่นิยม) มันจะบันเทิงตรงสูตรนี้นี่แหละ
สูตรคือ
log2(f/440Hz) = ?
n/12 = ?
n = ?x12
ตัวอย่างที่ 1
ถ้าอยากรู้ว่า 2000 Hz คือโน้ตอะไร ให้ทำดังนี้
log2(2000/440Hz) = 2.18442457114
n/12 = 2.18442457114
n = 2.18442457114x12
n = 26.2130948537 semitones
ตีเป็นเลขกลมๆก็คือปัดลงเป็น 26 semitones
2000 Hz อยู่สูงกว่า A4 อยู่ที่ 26 semitones
2000 Hz = B6
ตัวอย่างที่ 2
งั้นถ้าเป็น 1 Hz ล่ะ ก็ง่ายๆ ให้ทำดังนี้
log2(1/440Hz) = -8.78135971352
n/12 = -8.78135971352
n = -8.78135971352x12
n = -105.376316562 semitones
ตีเป็นเลขกลมๆก็คือปัดลงเป็น -105 semitones
1 Hz อยู่ต่ำกว่า A4 อยู่ที่ 105 semitones
1 Hz = C-4 (เผื่อใครยังไม่รู้ octave ติดลบ มีจริงนะครับ)
ตัวอย่างที่ 3 (เตรียมตัวเข้าสู่โหมดความบันเทิง)
0 Hz คือโน้ตอะไร ใครที่เคยอ่านกระทู้เก่าของผม น่าจะรู้คำตอบ แต่นั่นเป็นเพียงแค่ปากเปล่าจากผม ผมว่ามันอ้างว้างเกินไป
ผมว่าเรามาดูการแสดงวิธีทำพร้อมๆกันเลยดีกว่า ให้ทำดังนี้
log2(0/440Hz) = undefined (ไม่นิยาม)
อ้าว ทำไมถึงเป็นเช่นนี้ล่ะ แต่...... ช้าก่อน อย่าเพิ่งด่วนสรุป มันเป็นเพราะว่า
แม้ว่ากฎของ log2 ตัวตั้งต้องมากกว่า 0 ขึ้นไป
แต่คุณลองดูเว็บนี้นะ
https://calculator.academy/inverse-log-calculator/
inverse log คือการคำนวณย้อนกลับจาก log
แต่เราจะพูดถึงแต่เฉพาะ log2
โดยสูตร inverse log2 คือ x = logb-1(y) = b^ y
ผมจะให้คุณทำตามผมนะ ให้ทดลองทำแบบนี้ก่อน ถ้าคำนวณแล้วได้ 1 แปลว่าถูกต้อง

****************************************************************************************************************
คราวนี้ เราลองเปลี่ยนค่า Number (Y) จาก 0 เป็น -1074.99999999999988631 (ขี้เกียจใส่ทศนิยมเพิ่มละ เหอะๆๆ)
มันจะได้คำตอบแบบนี้
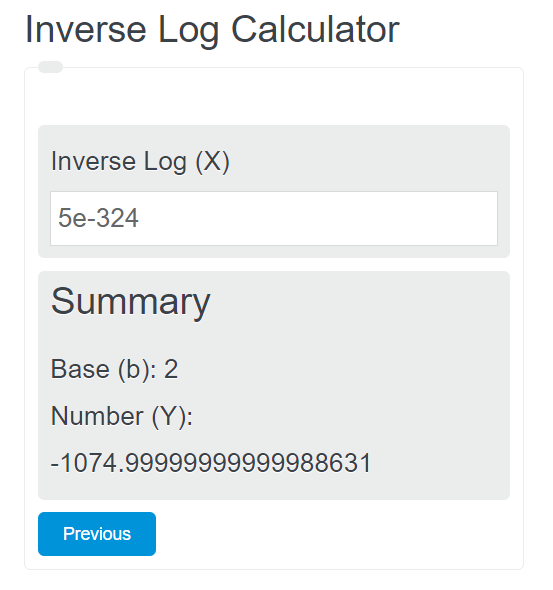
ซึ่งถ้าคุณเปลี่ยนกลับมาใช้สูตร log2(5e-324) มันก็จะได้คำตอบคือ -1074 (อ้างอิงจาก google) ที่จริงมันไม่ผิด เพราะเว็บ inverse log ก็ได้เท่านี้เหมือนกัน
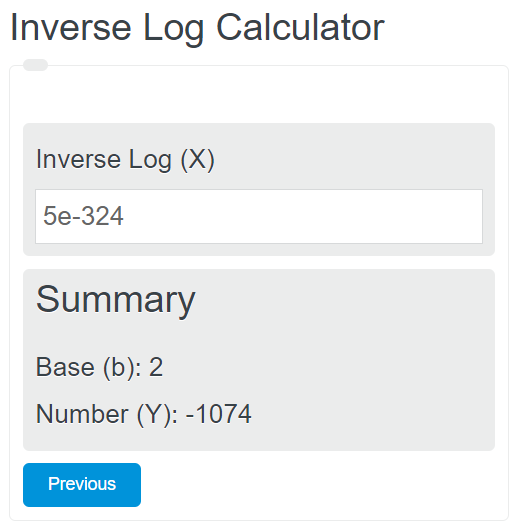
และที่ผมสังเกตคือ พอผมลองใส่ตั้งแต่ log2(5e-325) เป็นต้นไป google ไม่ให้คำตอบแล้วครับ เหมือนมันอิ่มตัวอะไรสักอย่าง
แล้วดูเว็บ inverse log สิครับ พอเข้าสู่ -1074.99999999999988632 เป็นต้นไป คำตอบมันเปลี่ยนแล้วครับ
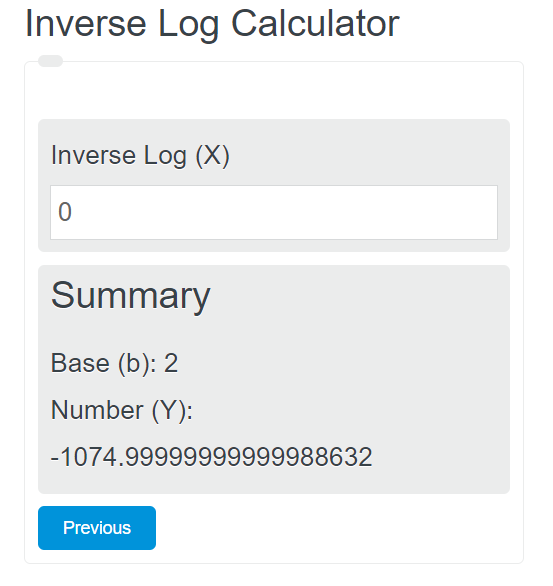
มันหมายความว่า มันเริ่มเข้าใกล้อนันต์แล้วครับผม (แม้ว่าทางทฤษฎีทั้งหมด อันนี้มันจะยังเป็นแค่เศษธุลีก็เถอะ)
มันก็เหมือนกับว่าถ้าดูรูปภาพที่ผมแสดงให้ดูเป็นหลัก
มันก็จะได้เป็น log2(0) = -1074.99999999999988632
แต่ที่จริงตัวตั้งมันไม่ใช่ 0
มันแค่เป็นจำนวนเล็กมากๆจนแทบจะเป็น 0 ต่างหาก
เพราะฉะนั้น ซึ่งมันก็เห็นกันแล้วใช่ไหม ว่ามันเข้าใกล้อนันต์ในเชิง log2 และเข้าใกล้ 0 ในเชิง inverse log2
มันก็เลยได้คำตอบเป็นดังนี้ อย่างไม่น่าสงสัยแล้ว (เว้นแต่ว่าเราไปเพิ่มเงื่อนไขเข้าไปอีก)
log2(0/440Hz) = ติดลบอนันต์ (-∞)
n/12 = -∞
n = -∞x12
n = -∞ semitones
0 Hz อยู่ต่ำกว่า A4 อยู่ที่ ∞ semitones
0 Hz = note-∞ (ในกรณีนี้จะไม่สามารถนิยามได้แล้วว่าเป็นตัวโน้ตอะไร แต่เรารู้ว่ามันอยู่ที่ octave ติดลบ infinity)
ที่คำตอบเป็นค่าติดลบ เพราะว่าค่า f ต่ำกว่าตัวตั้ง ซึ่งถ้าสูงกว่า คำตอบจะเป็นบวก แต่ถ้าคำ f เท่ากันกับตัวตั้ง (หารแล้วต้องเท่ากับ 1) คำตอบจะเป็น 0
0 Hz = ไม่มีเสียง เพราะไม่มีความถี่
ซึ่งถ้าเราไม่นับการใช้เทคนิคทางโปรแกรม หรือที่เรียกกันว่า mute หรือเกิดจากเทคโนโลยีต่างๆ (ซึ่งผมก็นึกไม่ออกอยู่ดี) ซึ่งไม่ใช่ธรรมชาติแรกแต่อย่างใด
0 Hz ในโลกนี้ ไม่มีจริงครับ
https://sciencing.com/earths-harmonic-resonate-frequencies-8600773.html
ส่วนถ้าใครอยากทำสถิติเป็นคนที่เสียงต่ำที่สุดในโลก ถ้าต้องการทำเสียง 0 Hz ก็คือไร้ความถี่นั่นเอง (note-∞)
คุณต้องไปอยู่ในสถานที่ที่หนึ่งของจักรวาลที่ไม่ใช่โลก แต่ผมจำไม่ได้แล้วว่ามันอยู่ที่ไหน รู้แค่ว่าผมเคยอ่านเรื่องนี้มาก่อน รู้สึกจะเป็นภาษาอังกฤษมั้ง ถ้าจำไม่ผิด สถานที่นั้นจะเป็นสถานที่ที่ไร้ความถี่ ถ้าคุณอยู่ที่นั่น คุณก็ไร้ความถี่ตามไปด้วย เพราะถ้าคุณยังมีความถี่ ก็เท่ากับว่าสถานที่นั้นมีความถี่ไปด้วย ซึ่งเกิดจากคุณ ซึ่งผมก็ไม่รับประกันว่าถ้าคุณอยู่ที่นั่นแล้ว คุณจะยังรอดชีวิตหรือเปล่า
****************************************************************************************************************
และที่มันบันเทิงยิ่งไปกว่านี้ก็คือ
ตัวอย่างที่ 4
แล้วถ้าความถี่เป็นติดลบล่ะ
สมมติว่าเป็น -440 Hz ก็ละกัน
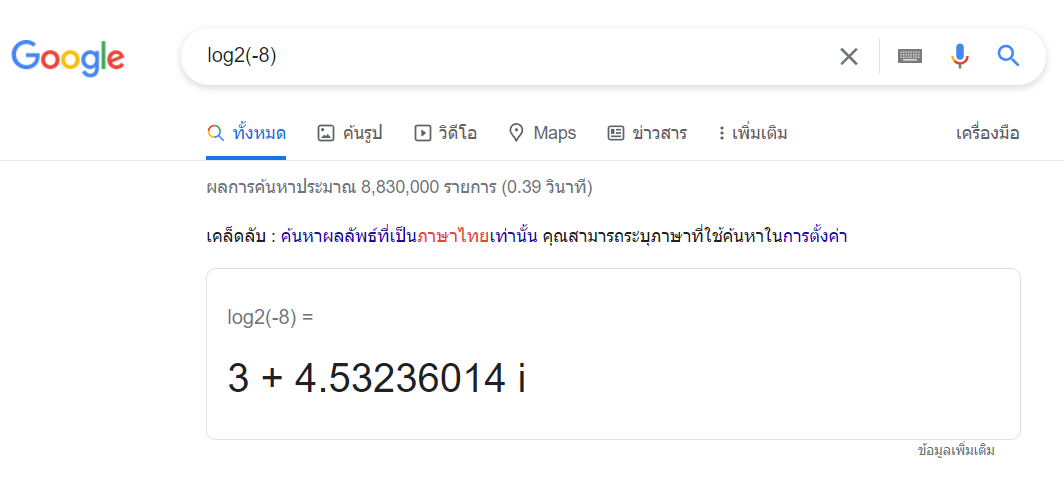
ปรากฏว่า Google สามารถให้คำตอบได้ครับ!!! ให้ทำดังนี้
log2(-440/440Hz) = 4.53236014 i
n/12 = 4.53236014 i
n = 4.53236014 i x 12
n = 54.3883217 i semitones
ตีเป็นเลขกลมๆก็คือปัดลงเป็น 54 i semitones
-440 Hz อยู่สูงกว่า A4 อยู่ที่ 54 i semitones
-440 Hz = Eb9 i (มันคือโน้ตอะไรฟะ!?!)
ในที่สุด ผมก็ก้าวผ่านความอนันต์สำเร็จเสียที (ในเชิงติดลบ)
แต่ผลลัพธ์ที่ได้ ดันเป็นบวกซะงั้น เออ ก็เอาเป็นว่า รู้ไว้ก็แล้วกัน ว่ามันเป็นแบบนี้จริงๆ
นี่คือหลักฐานครับ
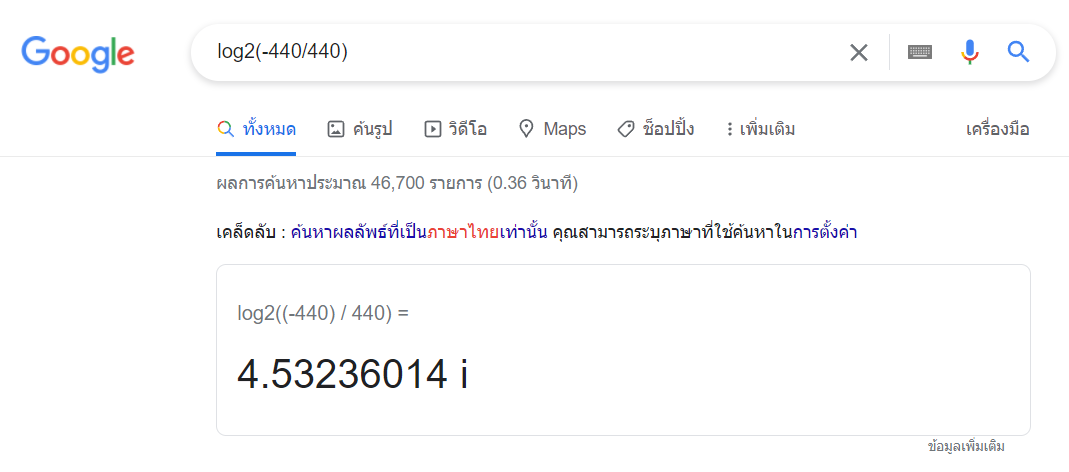
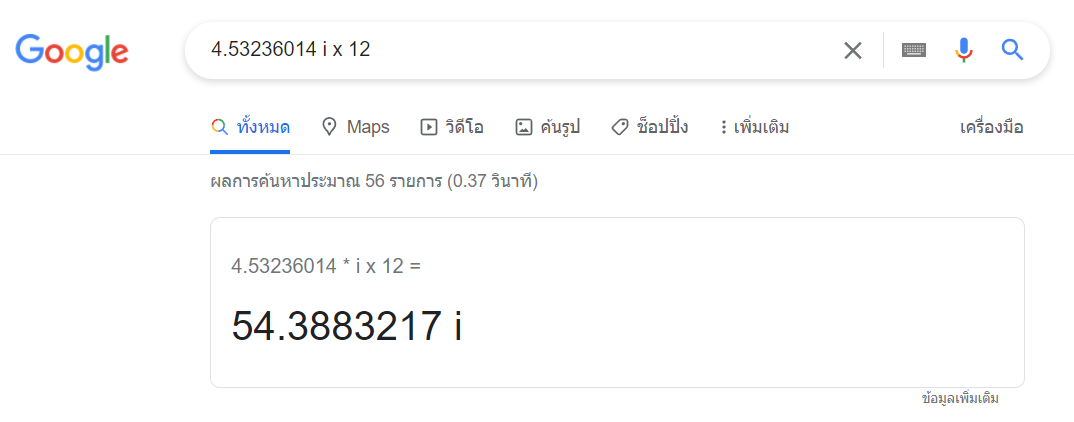
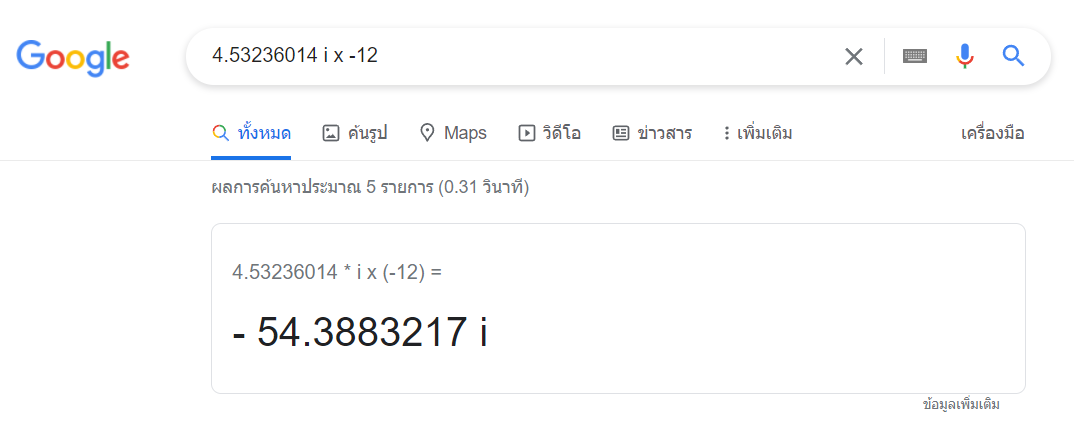
นี่ก็เป็นหลักฐานยืนยันแล้วนะครับว่า จุดจบของความไม่มีที่สิ้นสุด มีอยู่จริง (ช่างเป็นอะไรที่ย้อนแย้งสุดๆ)
ถ้าใครยังสงสัยว่ามันก้าวผ่านยังไงกัน ให้กลับไปดูค่า f ที่อยู่ข้างบนอีกทีครับ และลองดูตัวอย่างข้างบนแต่ละข้อครับผม
เดี๋ยวผมจะยกตัวอย่างง่ายๆอีก 2 ข้อ เพื่อเป็นการยืนยันว่า ผมไม่ได้โกงทฤษฎี
1) 5+2 น้อยกว่า 5+3 ใช่หรือไม่ ถ้าใช่ก็แสดงว่า 2 น้อยกว่า 3
2) 5-3 น้อยกว่า 5+0 ใช่หรือไม่ ถ้าใช่ก็แสดงว่า -3 น้อยกว่า 0
อ่อ นอกจากนี้ ผมยังมีรูปภาพแถมให้ดูเล่นๆอีกด้วย
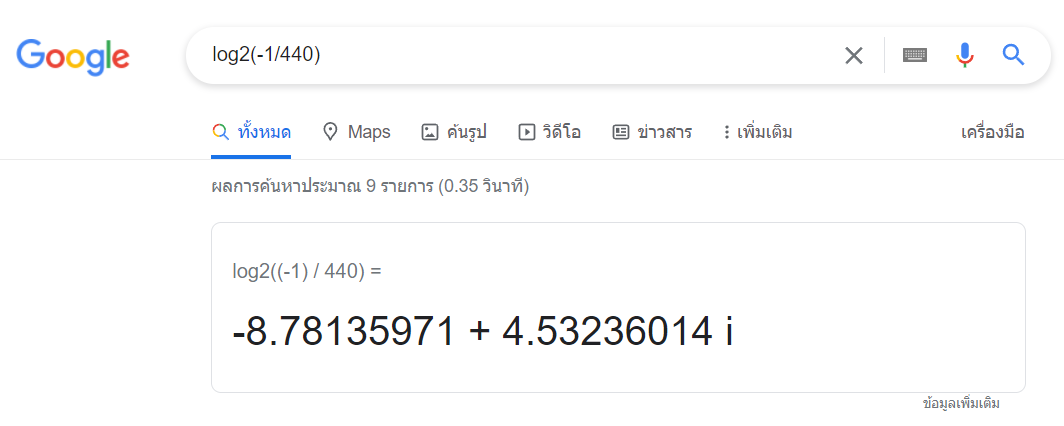
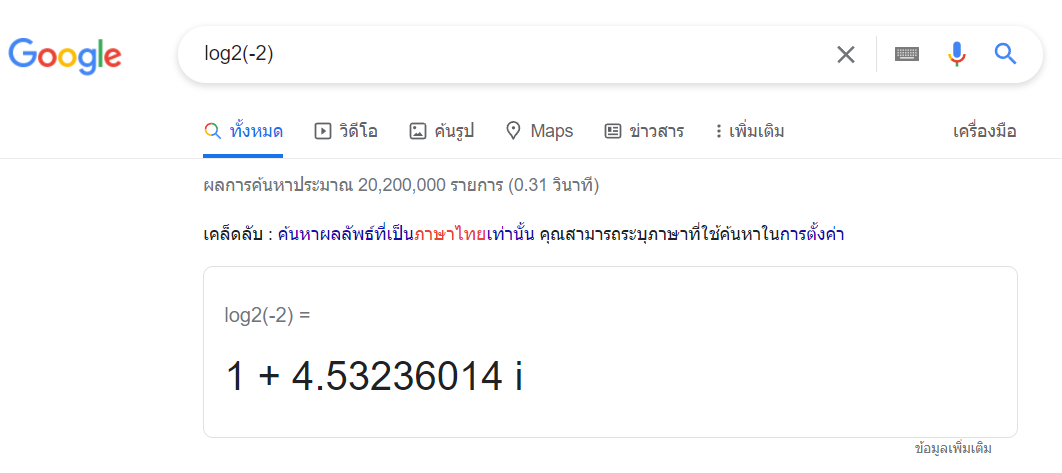




ความถี่ กับ โน้ตดนตรี และ การก้าวผ่านความอนันต์ (infinity)
https://th.wikipedia.org/wiki/%E0%B8%84%E0%B8%A7%E0%B8%B2%E0%B8%A1%E0%B8%96%E0%B8%B5%E0%B9%88
โน้ตดนตรีคืออะไร
https://th.wikipedia.org/wiki/%E0%B9%82%E0%B8%99%E0%B9%89%E0%B8%95%E0%B8%94%E0%B8%99%E0%B8%95%E0%B8%A3%E0%B8%B5
แล้วอนันต์คืออะไร (ในกรณีนี้ ไม่เกี่ยวข้องใดๆกับคนที่ชื่ออนันต์ทั้งสิ้น)
https://th.wikipedia.org/wiki/%E0%B8%AD%E0%B8%99%E0%B8%B1%E0%B8%99%E0%B8%95%E0%B9%8C
และที่ไม่น่าเชื่อ แต่ก็ต้องเชื่อ เพราะมันเกิดขึ้นจริง พิสูจน์โดยผมเอง แม้จะเป็นแค่เชิงทฤษฎีก็ตาม
ผมสามารถก้าวผ่านความอนันต์ได้ครับ โดยค้นพบจากสูตรที่เกี่ยวข้องกับความถี่และโน้ตดนตรี มันดูเหมือนจะเพ้อเจ้อสำหรับคนที่ไม่เชื่อเรื่องเหนือธรรมชาติ เพราะ ทุกสรรพสิ่งมีค่าเป็นอนันต์ ทุกอย่างที่มันเป็นไป มีเบื้องหลังคือพลังงานเสมอ แม้แต่เหตุการณ์ก่อนเกิดจักรวาลก็ตาม โดยมีเวลาเป็นระยะในความเป็นไปของพลังงาน
ซึ่งถ้าเอาชัดๆ คือ เวลา กับ พลังงาน มีค่าเป็นอนันต์ ไม่มีจุดเริ่มต้นและจุดจบ (ในกรณีที่ไม่ใช่ทฤษฎี beyond) หรือพูดง่ายๆ ก็คือ เป็นอมตะนั่นเอง
ทฤษฎี beyond จะเป็นแบบนี้ครับ สามารถหาจุดจบได้เสมอ แต่ก็สามารถเพิ่มข้อแม้ได้เสมอเช่นกัน เช่น เราค้นพบจุดจบแล้ว แล้วถ้างั้น จุดจบของจุดจบคืออะไร มันก็จะเกทับไปได้เรื่อยๆ เราอย่าพูดว่า จุดจบไม่มีจริง มันมีจริงครับ เพียงแต่ว่ามันเพิ่มข้อแม้ได้ก็เท่านั้นเอง
youtube อันนี้ อธิบายได้ดีมาก (ที่จริงสามารถไปต่อได้อีกนะ แต่เขาเลือกที่จะจบตรงนั้น)
ในคลิปนี้เป็นการก้าวผ่านความอนันต์โดยการเพิ่มข้อแม้จากคำศัพท์ต่างๆ
แต่วันนี้ ผมจะมาก้าวผ่านความอนันต์จากความถี่และโน้ตดนตรีครับผม
เข้าเรื่องจริงๆเสียที
คุณรู้จักความถี่ 440 Hz หรือเปล่า ถ้าใครยังไม่รู้จัก ผมจะอธิบายให้ตรงนี้เลย
มันคือความถี่มาตรฐานสากลของการทำดนตรีเพลงครับผม
เพลงต่างๆที่พวกเราฟังมักจะมีความถี่ 440 Hz
แต่บางคนก็ยึดติดกับ 432 Hz (flat กว่า 440) เพราะมันดูเป็นธรรมชาติกว่า บางคนบอกว่าเป็นความถี่เกี่ยวกับจักรวาล บางคนโยงไปถึงเรื่องลี้ลับ เรื่องศาสนา อะไรแบบเนี้ย ซึ่งก็ไม่รู้ว่าจริงเท็จแต่ประการใด อันนี้ผมไม่มีไอเดีย
โดยส่วนตัวแล้ว ผมก็ชอบหลากหลายครับ ไม่ว่าจะ flat หรือ sharp ก็ตาม ซึ่งมันก็ขึ้นอยู่กับอารมณ์อะนะ
ก่อนที่จะจริงจังไปมากกว่านี้ ก็อยากจะให้คนที่ยังไม่เคยรู้ ได้รู้เอาไว้ ว่า ความถี่ 440 Hz เท่ากับ โน้ต A4 ครับ
โอเค คราวนี้จะเข้มข้นของจริงละ เราจะมาเรียนรู้สูตรที่เกี่ยวข้องกับความถี่และโน้ตดนตรี
โดยวันนี้ ผมจะบอกทั้งหมด 2 สูตร คือ หาค่าความถี่จากโน้ตดนตรี และ หาค่าโน้ตดนตรีจากความถี่ (สูตรกลับ ซึ่งไม่นิยม)
โดยทั้ง 2 สูตรนี้ ต้องกำหนด 440 Hz (A4) เป็นตัวตั้ง
กำหนดให้ f คือ ค่าความถี่ (หน่วยเป็น Hz) และ n คือ ค่าโน้ตดนตรีที่เพิ่มขึ้นหรือลดลงจาก A4 เป็นหลัก (หน่วยเป็น semitone(s))
****************************************************************************************************************
หาค่าความถี่จากโน้ตดนตรี สูตรคือ f = 2^(n/12)x440Hz
ตัวอย่างที่ 1
ถ้าอยากรู้ว่า B4 คือความถี่เท่าไร ซึ่ง B4 สูงกว่า A4 อยู่ที่ 2 semitones ให้ทำดังนี้
f = 2^(2/12)x440Hz
f = 493.883301256 Hz
B4 = 493.883301256 Hz
ตัวอย่างที่ 2
คราวนี้เราลองไปไกลบ้าง งั้นเอาสัก F6 เลย ซึ่งสูงกว่า A4 อยู่ที่ 20 semitones ให้ทำดังนี้
f = 2^(20/12)x440Hz
f = 1396.91292573 Hz
F6 = 1396.91292573 Hz
ตัวอย่างที่ 3
ลองไปทางต่ำกันดูบ้าง A1 ก็ละกัน ซึ่งต่ำกว่า A4 อยู่ที่ 36 semitones ให้ทำดังนี้
f = 2^(-36/12)x440Hz
f = 55 Hz
A1 = 55 Hz
****************************************************************************************************************
หาค่าโน้ตดนตรีจากความถี่ (สูตรกลับ ซึ่งไม่นิยม) มันจะบันเทิงตรงสูตรนี้นี่แหละ
สูตรคือ log2(f/440Hz) = ?
n/12 = ?
n = ?x12
ตัวอย่างที่ 1
ถ้าอยากรู้ว่า 2000 Hz คือโน้ตอะไร ให้ทำดังนี้
log2(2000/440Hz) = 2.18442457114
n/12 = 2.18442457114
n = 2.18442457114x12
n = 26.2130948537 semitones
ตีเป็นเลขกลมๆก็คือปัดลงเป็น 26 semitones
2000 Hz อยู่สูงกว่า A4 อยู่ที่ 26 semitones
2000 Hz = B6
ตัวอย่างที่ 2
งั้นถ้าเป็น 1 Hz ล่ะ ก็ง่ายๆ ให้ทำดังนี้
log2(1/440Hz) = -8.78135971352
n/12 = -8.78135971352
n = -8.78135971352x12
n = -105.376316562 semitones
ตีเป็นเลขกลมๆก็คือปัดลงเป็น -105 semitones
1 Hz อยู่ต่ำกว่า A4 อยู่ที่ 105 semitones
1 Hz = C-4 (เผื่อใครยังไม่รู้ octave ติดลบ มีจริงนะครับ)
ตัวอย่างที่ 3 (เตรียมตัวเข้าสู่โหมดความบันเทิง)
0 Hz คือโน้ตอะไร ใครที่เคยอ่านกระทู้เก่าของผม น่าจะรู้คำตอบ แต่นั่นเป็นเพียงแค่ปากเปล่าจากผม ผมว่ามันอ้างว้างเกินไป
ผมว่าเรามาดูการแสดงวิธีทำพร้อมๆกันเลยดีกว่า ให้ทำดังนี้
log2(0/440Hz) = undefined (ไม่นิยาม)
อ้าว ทำไมถึงเป็นเช่นนี้ล่ะ แต่...... ช้าก่อน อย่าเพิ่งด่วนสรุป มันเป็นเพราะว่า
แม้ว่ากฎของ log2 ตัวตั้งต้องมากกว่า 0 ขึ้นไป
แต่คุณลองดูเว็บนี้นะ https://calculator.academy/inverse-log-calculator/
inverse log คือการคำนวณย้อนกลับจาก log
แต่เราจะพูดถึงแต่เฉพาะ log2
โดยสูตร inverse log2 คือ x = logb-1(y) = b^ y
ผมจะให้คุณทำตามผมนะ ให้ทดลองทำแบบนี้ก่อน ถ้าคำนวณแล้วได้ 1 แปลว่าถูกต้อง
****************************************************************************************************************
คราวนี้ เราลองเปลี่ยนค่า Number (Y) จาก 0 เป็น -1074.99999999999988631 (ขี้เกียจใส่ทศนิยมเพิ่มละ เหอะๆๆ)
มันจะได้คำตอบแบบนี้
ซึ่งถ้าคุณเปลี่ยนกลับมาใช้สูตร log2(5e-324) มันก็จะได้คำตอบคือ -1074 (อ้างอิงจาก google) ที่จริงมันไม่ผิด เพราะเว็บ inverse log ก็ได้เท่านี้เหมือนกัน
และที่ผมสังเกตคือ พอผมลองใส่ตั้งแต่ log2(5e-325) เป็นต้นไป google ไม่ให้คำตอบแล้วครับ เหมือนมันอิ่มตัวอะไรสักอย่าง
แล้วดูเว็บ inverse log สิครับ พอเข้าสู่ -1074.99999999999988632 เป็นต้นไป คำตอบมันเปลี่ยนแล้วครับ
มันหมายความว่า มันเริ่มเข้าใกล้อนันต์แล้วครับผม (แม้ว่าทางทฤษฎีทั้งหมด อันนี้มันจะยังเป็นแค่เศษธุลีก็เถอะ)
มันก็เหมือนกับว่าถ้าดูรูปภาพที่ผมแสดงให้ดูเป็นหลัก
มันก็จะได้เป็น log2(0) = -1074.99999999999988632
แต่ที่จริงตัวตั้งมันไม่ใช่ 0
มันแค่เป็นจำนวนเล็กมากๆจนแทบจะเป็น 0 ต่างหาก
เพราะฉะนั้น ซึ่งมันก็เห็นกันแล้วใช่ไหม ว่ามันเข้าใกล้อนันต์ในเชิง log2 และเข้าใกล้ 0 ในเชิง inverse log2
มันก็เลยได้คำตอบเป็นดังนี้ อย่างไม่น่าสงสัยแล้ว (เว้นแต่ว่าเราไปเพิ่มเงื่อนไขเข้าไปอีก)
log2(0/440Hz) = ติดลบอนันต์ (-∞)
n/12 = -∞
n = -∞x12
n = -∞ semitones
0 Hz อยู่ต่ำกว่า A4 อยู่ที่ ∞ semitones
0 Hz = note-∞ (ในกรณีนี้จะไม่สามารถนิยามได้แล้วว่าเป็นตัวโน้ตอะไร แต่เรารู้ว่ามันอยู่ที่ octave ติดลบ infinity)
ที่คำตอบเป็นค่าติดลบ เพราะว่าค่า f ต่ำกว่าตัวตั้ง ซึ่งถ้าสูงกว่า คำตอบจะเป็นบวก แต่ถ้าคำ f เท่ากันกับตัวตั้ง (หารแล้วต้องเท่ากับ 1) คำตอบจะเป็น 0
0 Hz = ไม่มีเสียง เพราะไม่มีความถี่
ซึ่งถ้าเราไม่นับการใช้เทคนิคทางโปรแกรม หรือที่เรียกกันว่า mute หรือเกิดจากเทคโนโลยีต่างๆ (ซึ่งผมก็นึกไม่ออกอยู่ดี) ซึ่งไม่ใช่ธรรมชาติแรกแต่อย่างใด
0 Hz ในโลกนี้ ไม่มีจริงครับ https://sciencing.com/earths-harmonic-resonate-frequencies-8600773.html
ส่วนถ้าใครอยากทำสถิติเป็นคนที่เสียงต่ำที่สุดในโลก ถ้าต้องการทำเสียง 0 Hz ก็คือไร้ความถี่นั่นเอง (note-∞)
คุณต้องไปอยู่ในสถานที่ที่หนึ่งของจักรวาลที่ไม่ใช่โลก แต่ผมจำไม่ได้แล้วว่ามันอยู่ที่ไหน รู้แค่ว่าผมเคยอ่านเรื่องนี้มาก่อน รู้สึกจะเป็นภาษาอังกฤษมั้ง ถ้าจำไม่ผิด สถานที่นั้นจะเป็นสถานที่ที่ไร้ความถี่ ถ้าคุณอยู่ที่นั่น คุณก็ไร้ความถี่ตามไปด้วย เพราะถ้าคุณยังมีความถี่ ก็เท่ากับว่าสถานที่นั้นมีความถี่ไปด้วย ซึ่งเกิดจากคุณ ซึ่งผมก็ไม่รับประกันว่าถ้าคุณอยู่ที่นั่นแล้ว คุณจะยังรอดชีวิตหรือเปล่า
****************************************************************************************************************
และที่มันบันเทิงยิ่งไปกว่านี้ก็คือ
ตัวอย่างที่ 4
แล้วถ้าความถี่เป็นติดลบล่ะ
สมมติว่าเป็น -440 Hz ก็ละกัน
ปรากฏว่า Google สามารถให้คำตอบได้ครับ!!! ให้ทำดังนี้
log2(-440/440Hz) = 4.53236014 i
n/12 = 4.53236014 i
n = 4.53236014 i x 12
n = 54.3883217 i semitones
ตีเป็นเลขกลมๆก็คือปัดลงเป็น 54 i semitones
-440 Hz อยู่สูงกว่า A4 อยู่ที่ 54 i semitones
-440 Hz = Eb9 i (มันคือโน้ตอะไรฟะ!?!)
ในที่สุด ผมก็ก้าวผ่านความอนันต์สำเร็จเสียที (ในเชิงติดลบ)
แต่ผลลัพธ์ที่ได้ ดันเป็นบวกซะงั้น เออ ก็เอาเป็นว่า รู้ไว้ก็แล้วกัน ว่ามันเป็นแบบนี้จริงๆ
นี่คือหลักฐานครับ
นี่ก็เป็นหลักฐานยืนยันแล้วนะครับว่า จุดจบของความไม่มีที่สิ้นสุด มีอยู่จริง (ช่างเป็นอะไรที่ย้อนแย้งสุดๆ)
ถ้าใครยังสงสัยว่ามันก้าวผ่านยังไงกัน ให้กลับไปดูค่า f ที่อยู่ข้างบนอีกทีครับ และลองดูตัวอย่างข้างบนแต่ละข้อครับผม
เดี๋ยวผมจะยกตัวอย่างง่ายๆอีก 2 ข้อ เพื่อเป็นการยืนยันว่า ผมไม่ได้โกงทฤษฎี
1) 5+2 น้อยกว่า 5+3 ใช่หรือไม่ ถ้าใช่ก็แสดงว่า 2 น้อยกว่า 3
2) 5-3 น้อยกว่า 5+0 ใช่หรือไม่ ถ้าใช่ก็แสดงว่า -3 น้อยกว่า 0
อ่อ นอกจากนี้ ผมยังมีรูปภาพแถมให้ดูเล่นๆอีกด้วย