คำตอบที่ได้รับเลือกจากเจ้าของกระทู้
ความคิดเห็นที่ 2
มันเป็นคอมโพสิทฟังก์ชัน(Composite Function) หาอนุพันธ์ได้โดยใช้กฏลูกโซ่(chain rule) ครับ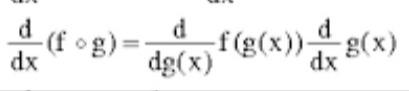 du/dt = d(u o v o s) (t) /dt
du/dt = d(u o v o s) (t) /dt
du/dt = du/dv × dv/ds × ds/dt
และสูตร e^ln(x) = x หรือ f o f^-1 (x) = x
ในเรื่องฟังก์ชันเอกซ์โพเนนเชียลกับฟังก์ชันลอการิทึม
6.1 Find du/dt = ?
du/dt = d(u o v o s) (t) /dt
du/dt = d(e^(ln(t^2)) )/dt
du/dt = (e^ln(t^2))(1/t^2)(2t)
du/dt = (2/t)(e^ln(t^2))
du/dt = 2(t^2 /t)
du/dt = 2t
ปล.จะคิดลัดแบบนี้ก็ได้ แต่ไม่ควรทำ
du/dt = d(e^(ln(t^2)) )/dt = d(t^2)/dt = 2t
6.2 Find du/dt |w=1
จากคำตอบข้อ 6.1
du/dt = 2t
du/dt |w = 2×(-|wI^2)
du/dt |w=1 = 2×(-(1)^2)
du/dt |w=1 = 2×(-1)
du/dt |w=1 = -2
ตารางสูตรหาอนุพันธ์
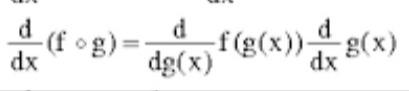 du/dt = d(u o v o s) (t) /dt
du/dt = d(u o v o s) (t) /dtdu/dt = du/dv × dv/ds × ds/dt
และสูตร e^ln(x) = x หรือ f o f^-1 (x) = x
ในเรื่องฟังก์ชันเอกซ์โพเนนเชียลกับฟังก์ชันลอการิทึม
6.1 Find du/dt = ?
du/dt = d(u o v o s) (t) /dt
du/dt = d(e^(ln(t^2)) )/dt
du/dt = (e^ln(t^2))(1/t^2)(2t)
du/dt = (2/t)(e^ln(t^2))
du/dt = 2(t^2 /t)
du/dt = 2t
ปล.จะคิดลัดแบบนี้ก็ได้ แต่ไม่ควรทำ
du/dt = d(e^(ln(t^2)) )/dt = d(t^2)/dt = 2t
6.2 Find du/dt |w=1
จากคำตอบข้อ 6.1
du/dt = 2t
du/dt |w = 2×(-|wI^2)
du/dt |w=1 = 2×(-(1)^2)
du/dt |w=1 = 2×(-1)
du/dt |w=1 = -2
ตารางสูตรหาอนุพันธ์

▼ กำลังโหลดข้อมูล... ▼
แสดงความคิดเห็น
คุณสามารถแสดงความคิดเห็นกับกระทู้นี้ได้ด้วยการเข้าสู่ระบบ



งงข้อนี้มากครับ
https://www.img.in.th/image/OTVHUS