คำตอบที่ได้รับเลือกจากเจ้าของกระทู้
ความคิดเห็นที่ 4
ขออธิบายไอเดียแค่ TREE(3) ละกัน
แปลมาจาก
https://www.popularmechanics.com/science/math/a28725/number-tree3/#:~:text=What%20is%20TREE(3)%3F,how%20many%20digits%20there%20are.
ในลิงค์คือเขาใช้คำว่า Tree กับ Seed แต่ Seed (เมล็ด) ขอเรียกว่า "จุด" แทน
TREE(3) ไอเดียมาจากเกมสร้างต้นไม้ง่ายๆโดยมีกฏ 2 ข้อ
1. ต้นแรกมีได้1จุด, ต้นที่สองมีได้สูงสุด, 2 จุด, ต้นที่สามมีได้สูงสุด 3 จุด, ... , ต้นที่ n มีได้สูงสุด n จุด, ...
2. ห้ามมีต้นไม้ซ้อนต้นไม้ หากเกิดกรณีแบบนี้ขึ้นคือจบเกม
TREE(n) = จำนวนวิธีสูงสุดที่เป็นไปได้จนกว่าจะจบเกม
TREE(1) มี 1 สี ใช้สีเขียว
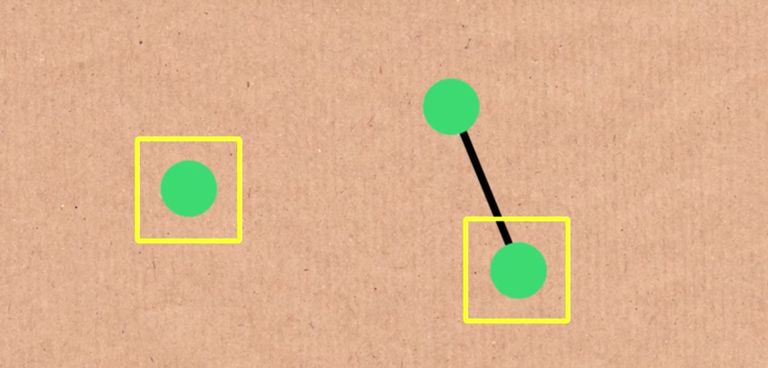
ต้นแรกใช้เขียว 1 จุด
ต้นที่สองไม่สามารถสร้างได้ (จะเขียว 1 จุด หรือ 2 จุดก็ไม่ได้เพราะผิดกฏข้อ 2)
จบเกมมีได้สูงสุด 1 วิธี ดังนั้น Tree(1) = 1
TREE(2) มี 2 สี ดำ-แดง (รูปจาก https://towardsdatascience.com/how-big-is-the-number-tree-3-61b901a29a2c )
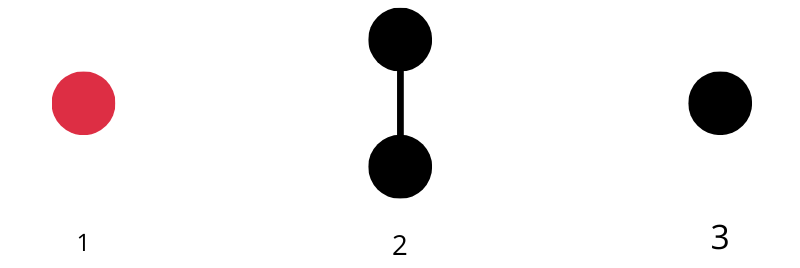
ต้นแรกใช้สีแดง 1 จุด
ต้นที่สองจะเป็นดำกับดำ(แดง-แดง หรือดำ-แดงไม่ได้เพราะผิดกฏข้อ2 หรือถ้าใช้ดำ 1 จุดต้นที่3 จะสร้างไม่ได้)
ต้นที่สามเป็นดำ 1 จุด
ต้นที่สี่ ไม่สามารถสร้างได้
จบเกมมีสูงสุดได้ 3 วิธี ดังนั้น TREE(2)=3
TREE(3)มี 3 สีใช้เขียว-แดง-ดำ
เราจะพบว่าจำนวนวิธีที่เป็นไปได้มันเยอะมาก ขอใส่รูปตามในลิงค์แทน
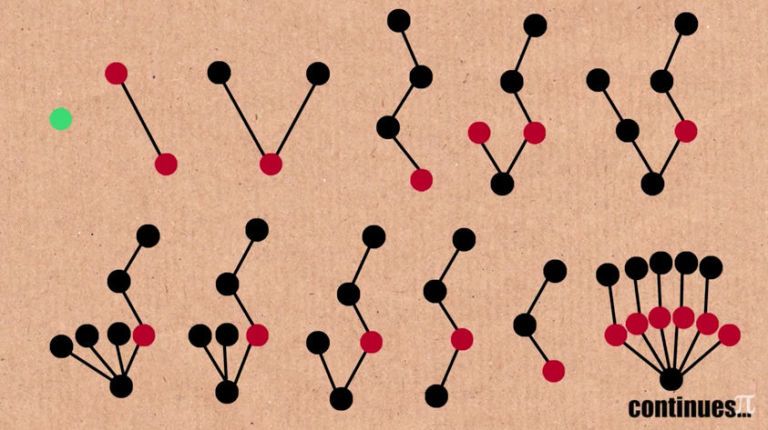
ผมก็นึกภาพไปเรื่อยๆไม่ออกเหมือนกันว่า Tree(3) มัน finite ยังไง
ส่วนวิธีพิสูจน์ว่าค่า Tree(3) มากกว่า Graham number คงต้องใช้คณิตศาสตร์ขั้นสูงคำนวณ แต่เท่าที่หาข้อมูลมามีคนบอกว่า Tree(3) ไม่สามารถเขียนออกมาเป็นค่าที่แน่นอนทางคณิตศาสตร์ได้ ทำได้แค่เปรียบเทียบเป็นช่วงกับจำนวนอื่น
แปลมาจาก
https://www.popularmechanics.com/science/math/a28725/number-tree3/#:~:text=What%20is%20TREE(3)%3F,how%20many%20digits%20there%20are.
ในลิงค์คือเขาใช้คำว่า Tree กับ Seed แต่ Seed (เมล็ด) ขอเรียกว่า "จุด" แทน
TREE(3) ไอเดียมาจากเกมสร้างต้นไม้ง่ายๆโดยมีกฏ 2 ข้อ
1. ต้นแรกมีได้1จุด, ต้นที่สองมีได้สูงสุด, 2 จุด, ต้นที่สามมีได้สูงสุด 3 จุด, ... , ต้นที่ n มีได้สูงสุด n จุด, ...
2. ห้ามมีต้นไม้ซ้อนต้นไม้ หากเกิดกรณีแบบนี้ขึ้นคือจบเกม
TREE(n) = จำนวนวิธีสูงสุดที่เป็นไปได้จนกว่าจะจบเกม
TREE(1) มี 1 สี ใช้สีเขียว

ต้นแรกใช้เขียว 1 จุด
ต้นที่สองไม่สามารถสร้างได้ (จะเขียว 1 จุด หรือ 2 จุดก็ไม่ได้เพราะผิดกฏข้อ 2)
จบเกมมีได้สูงสุด 1 วิธี ดังนั้น Tree(1) = 1
TREE(2) มี 2 สี ดำ-แดง (รูปจาก https://towardsdatascience.com/how-big-is-the-number-tree-3-61b901a29a2c )

ต้นแรกใช้สีแดง 1 จุด
ต้นที่สองจะเป็นดำกับดำ(แดง-แดง หรือดำ-แดงไม่ได้เพราะผิดกฏข้อ2 หรือถ้าใช้ดำ 1 จุดต้นที่3 จะสร้างไม่ได้)
ต้นที่สามเป็นดำ 1 จุด
ต้นที่สี่ ไม่สามารถสร้างได้
จบเกมมีสูงสุดได้ 3 วิธี ดังนั้น TREE(2)=3
TREE(3)มี 3 สีใช้เขียว-แดง-ดำ
เราจะพบว่าจำนวนวิธีที่เป็นไปได้มันเยอะมาก ขอใส่รูปตามในลิงค์แทน

ผมก็นึกภาพไปเรื่อยๆไม่ออกเหมือนกันว่า Tree(3) มัน finite ยังไง
ส่วนวิธีพิสูจน์ว่าค่า Tree(3) มากกว่า Graham number คงต้องใช้คณิตศาสตร์ขั้นสูงคำนวณ แต่เท่าที่หาข้อมูลมามีคนบอกว่า Tree(3) ไม่สามารถเขียนออกมาเป็นค่าที่แน่นอนทางคณิตศาสตร์ได้ ทำได้แค่เปรียบเทียบเป็นช่วงกับจำนวนอื่น
แสดงความคิดเห็น


จำนวนที่ใหญ่กว่า graham number เช่น tree(3) rayo number scg(13) sscg(3) infinityหลายประเภทมีหลักการทำงานอย่างไรหรอครับ